In the last part of our series "Why You Shouldn't Roll Your Own Cryptography," I talked about a custom hashing algorithm using Triple-DES. Today, I'll present another case from a desktop application that used a completely custom "hashing" algorithm. It's important to note that the application was written in a native language, so some reverse engineering will be involved.

But before we dive in, let's clear up some terms: encoding, hashing, and encryption. We’ll explore what this algorithm really is by the end of this article.
HASHING is the process of turning input data like text, files, or passwords into a fixed-size string of characters, known as a hash value or hash code. This is done by a hash function, which produces a unique output for each unique input.

ENCRYPTION is the process of turning plaintext (unencrypted data) into ciphertext (encrypted data) using an encryption algorithm and a key. The ciphertext usually looks random and can only be turned back into readable plaintext by someone with the right key.

ENCODING is about changing data from one format to another, usually to make it usable in different systems or software. Unlike encryption, encoding isn’t about security or keeping data safe; it’s about compatibility and readability.

With these ideas in mind, let's start the analysis. We'll look at what happens to our example password, "1qaz2wsx3edc," by following the operations in a DLL file named password.dll. I used tools like x64dbg and Binary Ninja to begin dissecting the function labeled CheckP:



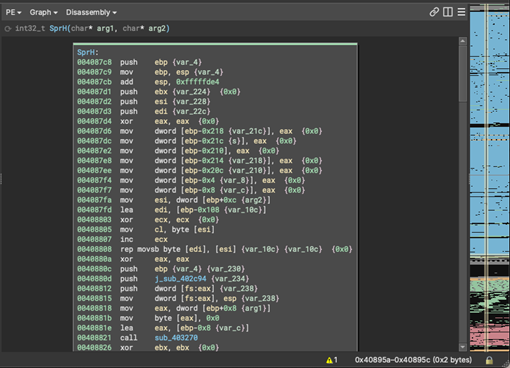
1. Password processing can be divided into two stages. In the first stage, the following steps are performed:

a. The password character is stored in the EAX register. This register stores the numerical value corresponding to the character in the ASCII table (instruction at address 0x00408845).

b. Then the transformation occurs (instructions at addresses 0x00408847 to 0x0040884b).
charcode=charcode+charcode+i-10
where i is the position of that charcode,counting from 1

c. The resulting value should now be converted into a string. That is, in this case, 89 to "89". The difference is that the value 89 is an ordinary number, and "89" is two characters "8" and "9" (instructions at addresses 0x0040884e to 0x00408867).



d. These points must be repeated for each character of the password, and the result is the following string:


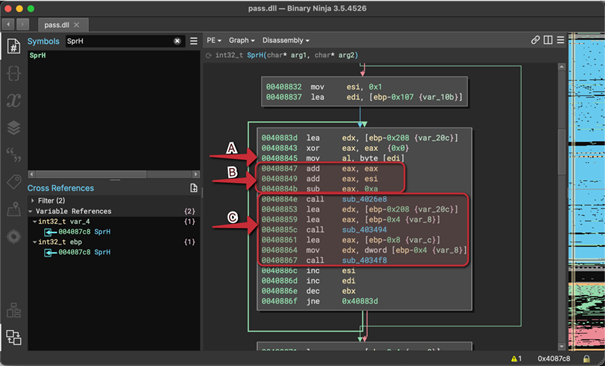
The result of the first stage is passed to the next stage, where successively:

e. Two digits are taken from the received decimal representation string, which are again converted to the actual value, i.e. the string "89" to the number 89 (instructions at addresses 0x00408894 to 0x004088a2).

f. If the value is less than 40 then three digits are taken instead (instructions at addresses 0x004088a7 to 0x004088b7).



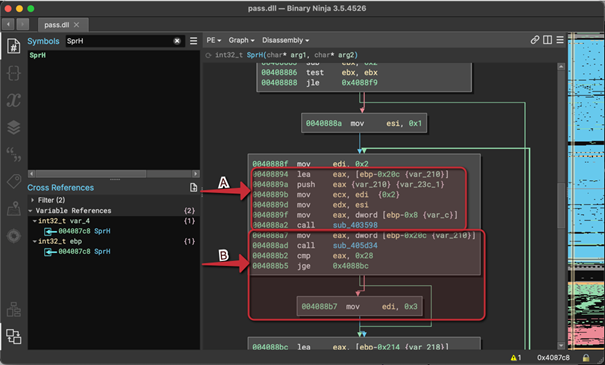
g. The resulting number is converted into a hexadecimal representation. That is, in the case of the number 89, it will be 0x59 (instructions at addresses 0x004088bc to 0x004088f7), and then to a string of characters, which in this case is "59".



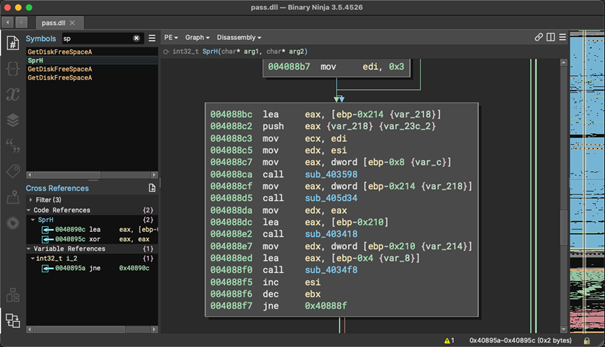
h. This process is repeated n - 2 many times, where n is the number of digits in the resulting string, and at each iteration of the loop, the processing "window" is moved by one position. This means that on the first iteration the first and second digits will be checked, and on the second iteration the second and third digits will be checked. As a result of the above, a final password form is obtained:



2. This creates a final form of the password, which is then compared with what is in the database, and the application decides on authorization based on this.

To simplify the analysis, the algorithm can be presented as code in Python:

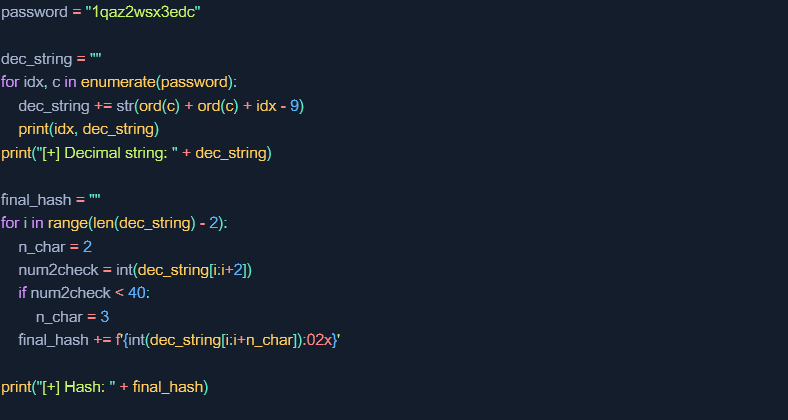
Attack #1 – full password restoration

The process outlined above can be easily reversed if you adopt a few properties that are sufficient to handle most cases, but this is not an exhaustive method. It is only meant to show that this is a threat to the confidentiality of the processed data. For the sake of example, let's assume that we have the example “final form” (1qaz2wsx3edc) given earlier:



To recover the password from it, follow the steps below:

1. Convert hexadecimal to decimal. Start by converting two hexadecimal numbers into decimal. For example, "59" converts to decimal 89. Here's what to consider:

a. "A" hexadecimal number that starts with "1". Just as during the transformation process, when the number was less than 40, the third digit had to be taken, so in the process of recovering the password, this should also be considered.
The first printable character (space) has a value of 32. And after additional transformations (mentioned during transformation), the minimum value that can be obtained is 32 + 32 + 1 - 10 = 55, or 0x37, so the number will not start with a hexadecimal "1", and the closest value with a hexadecimal one in front is 0x100, or 256. So, you can assume at this point that if the value starts with a hexadecimal "1", it means that the number at the conversion was composed of three decimal digits. It is necessary to take three hexadecimal digits and only convert them to decimal.

b. If the previous number had a "0" in the middle, the leading "1" could mean it was originally a three-digit number starting with "0". In such cases, consider only the last two digits for conversion..

2. Move through the data sequence, converting each segment. This yields an array of decimal values that need to be sequentially aligned.



3. However, it is necessary to consider in this process that the numbers overlap. Using the example of the first three decimal numbers obtained above:

a. 0x59 converts to 89,
b. 0x5c converts to 92,
c. 0xda converts to 218.
You can see a relation that the last digit of a number is the first digit of the next number. For this reason, you can't just link them together and you need to get rid of these repeats. The entire restoration process is represented by the following code in Python (where decimals is the resulting array with the recovered decimal values):



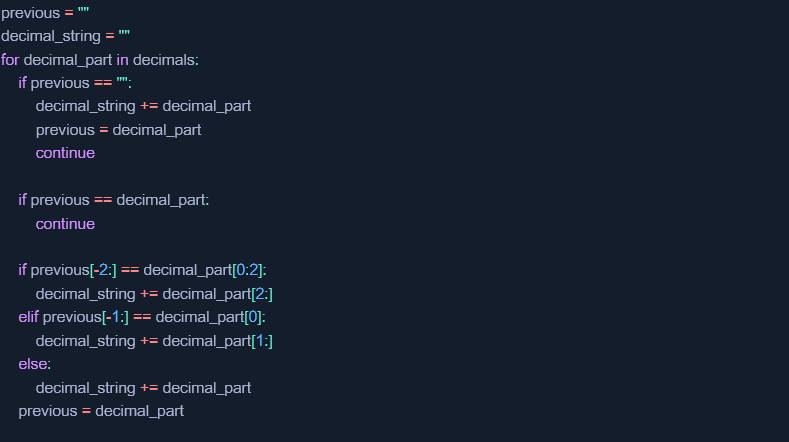
Thus, we get the following sequence of digits:



4. In the last step, you need to convert the resulting string of digits into a password. In this case, you also need to consider two cases:

a. A two-digit number.
b. A three-digit number.

It is useful to consider both cases at the same time but considering them in turn gives sufficient effect. Starting with the first variant, if the number after inverting the formula below gives a value between 32 and 126, it means that the character will be printable. If not, then take the third digit.

charcode=charcode+charcode+i-10
where i is the position of that charcode,counting from 1

Using the presented method, we managed to gain access to the user account of Administrator.
Below is the full code implementing the entire method in Python:

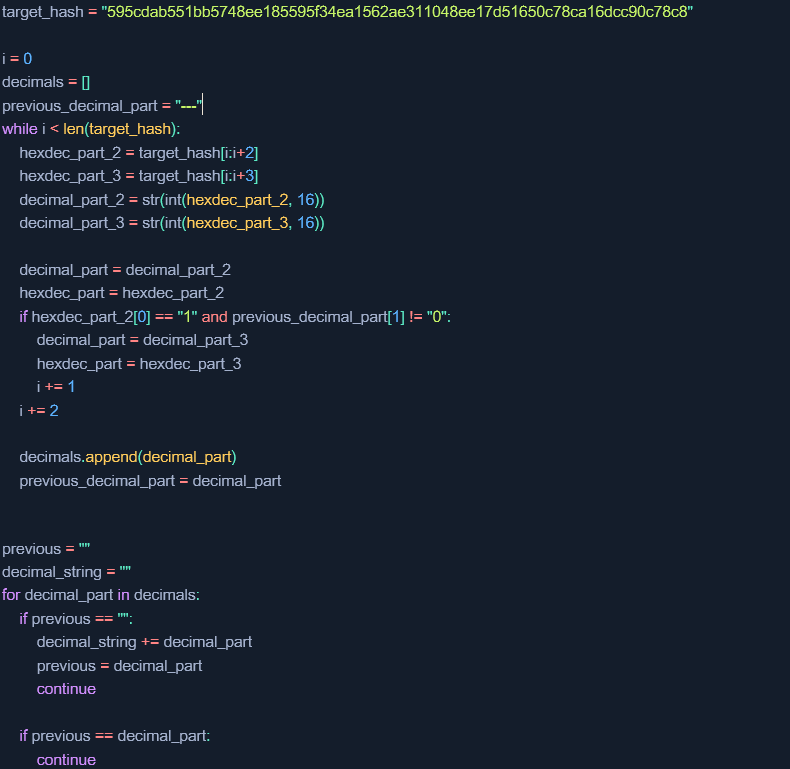
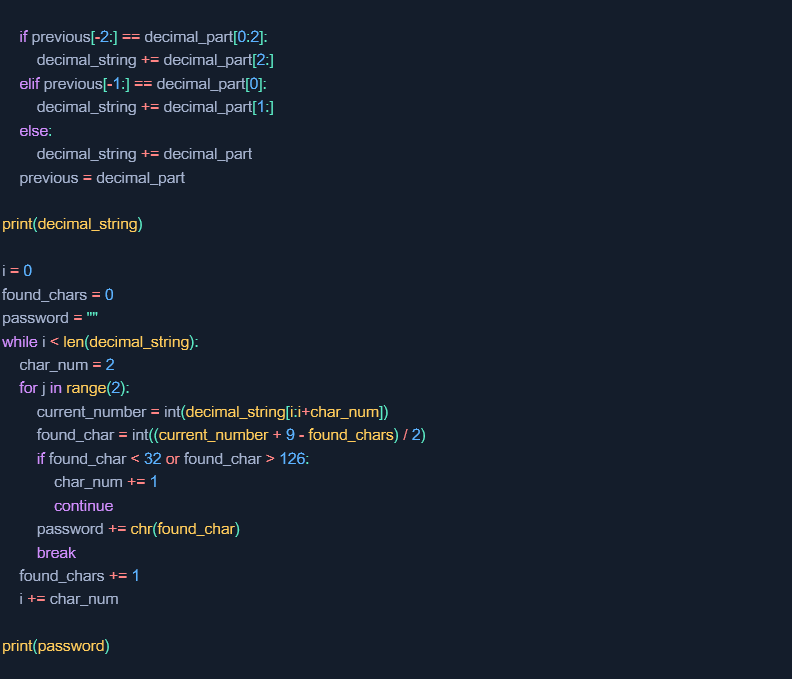
Attack #2 – guessing the password two characters at a time

This method involves guessing combinations of two characters, which, when encrypted, will return a result that will be the initial fragment of the password ciphertext. In this way, instead of having to guess the whole password, it is enough to guess fragments every two characters. Below is a list of steps that demonstrate the method:

1. We will again use the example of the password 1qaz2wsx3edc, the ciphertext of which is:



First, iterate through all combinations of two printable characters starting with a space, so the first candidate for a password would be two spaces whose ciphertext is:



2. The indicated ciphertext is not similar to the beginning of the target ciphertext, so continue iterating, the next character will be an exclamation mark (!). Now the password candidate will be (space and exclamation point):



The ciphertext will also be (the problem is described in Attack #3):



3. Continue the iteration until the final candidate is 1q and the ciphertext is:



Identically, the target ciphertext begins:



4. When you have successfully found the first characters of the password then move on to the next ones, until finally you get a ciphertext identical to the target one.

Below is the full code implementing the entire method in Python:

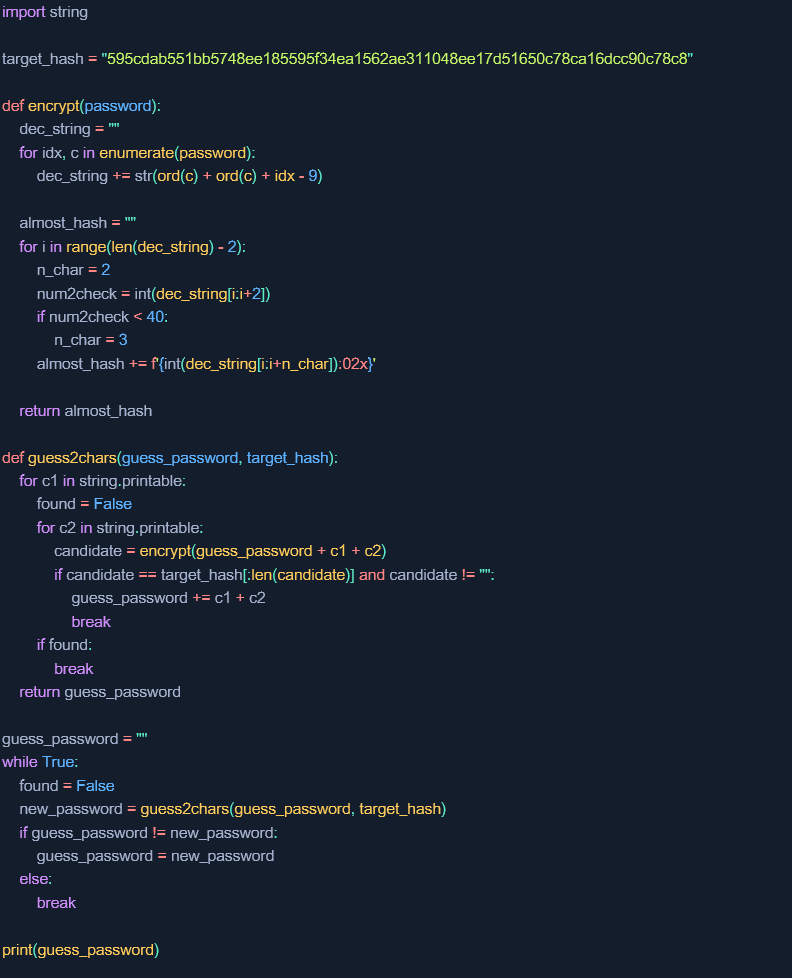
Attack #3 – collision

A collision is a vulnerability of a cryptographic algorithm in which two different plaintexts produce the same ciphertexts. In the case of this algorithm, it considers the digits of the entire decimal sequence. For this reason, in certain cases the last character is less important than the others. Below is an example of a collision:

1. Password: 1qaz2
Final form: 595cdab551bb5748ee18559

2. Password: 1qaz3
Final form: 595cdab551bb5748ee18559

3. Password: 1qaz4
Final form: 595cdab551bb5748ee18559

So, what is that?

I have intentionally used phrases like "Final Form," "Processing," "Transformation" throughout the text so as not to impose on anyone what the algorithm actually is. Let's list all the features that will allow us to identify this algorithm:

1. The length of the final form of the password is variable and depends on the password itself.

2. The only input to this algorithm is the password.

These two features alone allow us to eliminate two of the three candidates. Most hashing algorithms have fixed-size output (the exception is PBKDF2, which allows you to define the hash length) and are irreversible. Encryption, on the other hand, uses a cryptographic key, which is an essential element of the whole algorithm - here such a key is missing.
So by the method of exclusion, we can conclude that this algorithm is nothing more than an over-complicated way to encode data. It's a bit like trying to store passwords in Base64. That's not what this algorithm was created for.

Ultimate remediation

Use secure hashing algorithms to store passwords in the database, which are additionally resistant to GPU and FPGA/ASIC attacks. The best choice in this case will be Argon2id, if you do not have the ability to implement it in your application choose scrypt. When choosing the right input parameters, I encourage you to read the OWASP recommendations:

• https://cheatsheetseries.owasp.org/cheatsheets/Password_Storage_Cheat_Sheet.html

Summary

The article begins by defining key terms: encoding, hashing, and encryption, to ensure clarity for all readers. It then dives into a detailed analysis of a custom "hashing" algorithm discovered in a desktop application. This algorithm, rather than using standard cryptographic practices, employs a multi-step transformation process to convert passwords into a so-called hashed form.

The case study methodically unpacks the algorithm's complex operations, showcasing how passwords undergo various transformations before reaching their final form. The analysis reveals two significant vulnerabilities that could be exploited due to the algorithm's design flaws, highlighting the inherent risks of its use.
Most critically, the text reveals that what was intended as a hashing algorithm functions more as an intricate encoding mechanism. This misclassification introduces potential security risks, as the method lacks the robustness of true cryptographic hashing or encryption.
The article concludes by stressing the importance of adhering to established cryptographic standards and avoiding the pitfalls of custom solutions without sufficient cryptographic expertise. Through this comprehensive exploration, the reader is left with a clear understanding of the dangers posed by inadequately designed cryptographic mechanisms.

More information:
• https://owasp.org/www-project-developer-guide/draft/07-implementation/04-dos-donts/03-cryptographic-practices
• https://www.researchgate.net/publication/353210621_You_Really_Shouldn't_Roll_Your_Own_Crypto_An_Empirical_Study_of_Vulnerabilities_in_Cryptographic_Libraries


#Cybersecurity #DoSAttack #WebSecurity #Pentesting #InfoSec #PentestChronicles